参考文章
《概率论与数理统计》浙大版（第四版）教材
百度百科

基本概念

条件概率

条件概率是指事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为：P（A|B），读作“在B的条件下A的概率”。条件概率可以用决策树进行计算。若只有两个事件A，B，那么$$P(A|B)=\frac{P(A|B)}{P(B)}$$

概率测度

如果事件 B 的概率 P(B) > 0那么 Q(A) = P(A | B) 在所有事件 A 上所定义的函数 Q 就是概率测度。
如果 P(B) = 0 P(A | B) 没有定义。条件概率可以用决策树进行计算。

基本定理

定理1

设A，B 是两个事件，且A不是不可能事件，则称 $P(B|A)=\frac{P(AB)}{P(A)} $ 为在事件A发生的条件下，事件B发生的条件概率。一般地,$P(B|A) \neq P(B) $，且它满足以下三条件：
（1）非负性；（2）规范性；（3）可列可加性。

定理2

设E 为随机试验，Ω 为样本空间，A，B 为任意两个事件，设P(A)>0，称 $P(B|A)=\frac{P(AB)}{P(A)} $ 为在“事件A 发生”的条件下事件B 的条件概率。
上述乘法公式可推广到任意有穷多个事件时的情况。
设 $ A_1, A_2 \ldots A_n $ 为任意 n 个事件（n≥2）且 $ P(A_1, A_2 \ldots A_n ) > 0$则 $ P(A_1, A_2 \ldots A_n ) =P(A_1)P(A_2|A_1) \ldots P(A_n|A_1 A_2 \ldots A_{n-1}) $

定理3 （全概率公式）

如果事件$B_1、B_2、B_3 \ldots B_n$ 构成一个完备事件组，即它们两两互不相容，其和为全集；并且P（Bi)大于0，则对任一事件A有
$P(A)=P(A|B_1)P(B_1) + P(A|B_2)P(B_2) + \ldots + P(A|B_n)P(B_n) = \sum_{i=1}^{n} P(A_i)(B|A_i) $
特别地，对于任意两随机事件A和B，有如下成立
$P(B)=P(B|A)P(A) + P(B|\overline A)P(\overline A)$

定理4 （贝叶斯公式）

通常，事件A在事件B(发生)的条件下的概率，与事件B在事件A的条件下的概率是不一样的；然而，这两者是有确定的关系,贝叶斯法则就是这种关系的陈述。
$P(A_i|B) = \frac{P(B|A_i)P(A_i)}{\sum_{i=1}^{n} P(B|A_i)P(A_i)} $

例题一

$P(A)=\frac{1}{4}, P(B|A)=\frac{1}{3},P(A|B)=\frac{1}{2},求 P(A \cup B),P(; \bar{A} ; |A \cup B) $

解：
$ P(B|A) = \frac{P(A \cap B)}{P(A)} = \frac{1}{3} $
$ P(A|B) = \frac{P(A \cap B)}{P(B)} = \frac{1}{2} $
$ P(A \cap B) = P(A)P(B|A) = \frac{1}{12} $
$ P(A) = \frac{1}{4} $
$ P(B) = \frac{1}{6} $
$ P(A \cup B) = P(A) + P(B) - P(A \cap B) = \frac{1}{3} $
$P(; \bar{A} ; |A \cup B) = \frac{P({B}-P(A \cap B))}{P(A \cup B)} = \frac{1}{4}$

例题二

一个盒子有五个红球，四个白球，采用不放回抽样，每次取一个，取三次。
（1）求前两次中至少有一次取到红球的概率
（2）已知前两次中至少有一次取到红球，求前两次中恰有一次取到红球的概率
（3）求第1，2次取到红球，第三次取到白球的概率

解：
设
$A_i=\begin{Bmatrix}第i次取到红球事件\end{Bmatrix}$
$B=\begin{Bmatrix}前面两次当中至少有一次取得红球\end{Bmatrix}$
$C=\begin{Bmatrix}前面两次当中恰好有一次取得红球\end{Bmatrix}$
则
$P(B) = 1 - P(\overline{B}) = 1- P(\overline{A_1})P(\overline{A_2}|\overline{A_1}) = 1 - \frac{4}{9} \times \frac{3}{8} = \frac{5}{6} $
$P(C) = 1- P(A_1 A_2|B) = \frac{2}{3} $
$P(A_1 A_2 \overline{A_3}) = \frac{5}{9} \times \frac{4}{8} \times \frac{4}{7}= \frac{10}{63} $

例题三

某人参加某种考核，已知第一次参加能通过的概率是60%，若第一次未通过，第二次参加能通过的概率是70%，若前两次未通过，第二次参加能通过的概率是80%，求此人最多三次就能通过考核的概率。
解：
设
$A_i=\begin{Bmatrix}第i通过考核\end{Bmatrix}$

$ 1 - P(\overline{A_1}\overline{A_2}\overline{A_3}) = 1 - 0.4 \times 0.3 \times 0.2 = 0.976 $

例题四

一小学举办家长开放日，欢迎家长参加活动，小明的母亲参加的概率为80%，若母亲参加，则父亲参加的概率为30%，若母亲不参加，则父亲参加的概率为90%。
（1）求父母都参加的概率
（2）求父母参加的概率
（3）在已知父亲参加的条件下，求母亲参加的概率

解：
设
$A=\begin{Bmatrix}母亲参加\end{Bmatrix}$
$B=\begin{Bmatrix}父亲参加\end{Bmatrix}$
$P(A) = 0.8$
$P(B|A)=0.3$
$P(B|\overline{A}) = 0.9$
$P(B|A)= \frac{P(AB)}{P(A)} = 0.3 => P(AB)=0.24$
$P(B)= P(A)P(B|A) + P(\overline{A})P(B|\overline{A}) = 0.8 \times 0.3 + 0.2 \times 0.9 = 0.42 $
$P(A|B)= \frac{P(AB)}{P(B)} = \frac{4}{7} $

例题五

有甲乙两盒，甲盒有三个红球两个白球，乙盒有两个红球，一个白球。先从甲盒中采用不放回抽样取3球放入到乙盒，再从乙盒中取一个球，球取到的是红球的概率。
解：
设
$A=\begin{Bmatrix}甲盒中取球\end{Bmatrix}$
$B=\begin{Bmatrix}乙盒中去球\end{Bmatrix}$
$
P(B)=P(B|A_1) \times P(A_1) + P(B|A_2) \times P(A_2) + P(B|A_3) \times P(A_3) = \\
\frac{1}{2} \times \frac{C_{3}^{1}C_{2}^{2}}{C_{5}^{3}} + \frac{2}{3} \times \frac{C_{3}^{2}C_{2}^{1}}{C_{5}^{3}} + \frac{5}{6} \times \frac{C_{3}^{3}}{C_{5}^{3}} = \frac{19}{30} \\
$

例题六

根据以往的临床记录某种诊断癌症的试验具有5%的假阳性以及%3的假阴性
若设
A={试验反应是阳性} C={被诊断患有癌症}
则有

$P(A| \overline{C}) = 5% $
$P(\overline{A}|C) = 3% $

已知某一群体P(C) = 0.005,问这种方法能否用于普查。

$
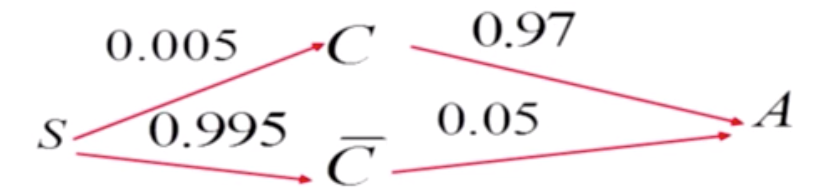
P(C|A) = \frac{P(CA)}{P(A)} = \frac{P(CA)}{P(A|C)P(C) + P(A|\overline{C})P(\overline{C})} = 0.08882783882783883
$